Reduced-order nonlinear solutions (RONS)
To approximate solutions of a PDE we consider an ansatz which depends on space and also nonlinearly on time-dependent parameters. RONS provides a framework for evolving these parameters, where the ODEs obtained for the parameters minimize the instantaneous discrepancy between reduced dynamics and the full PDE dynamics.
We have managed to successfully apply RONS to several problems, including vortices in 2D ideal fluid flow and the nonlinear Schrödinger equation for deep water waves, and the Fokker-Planck equation.
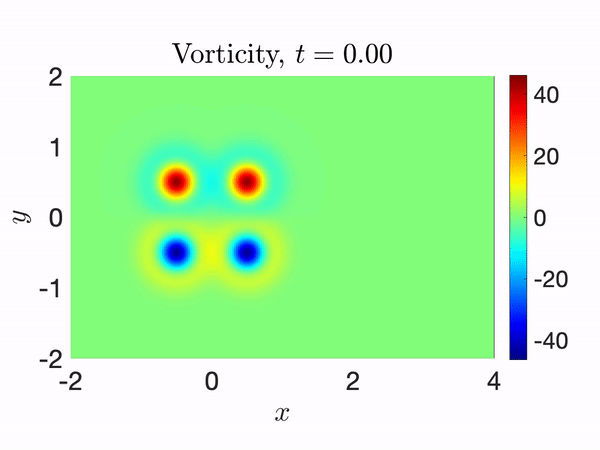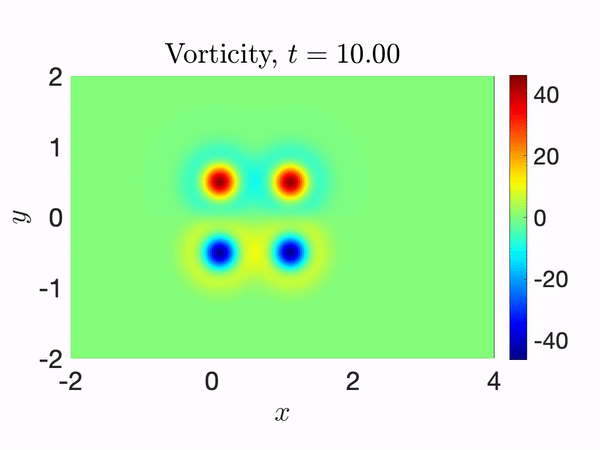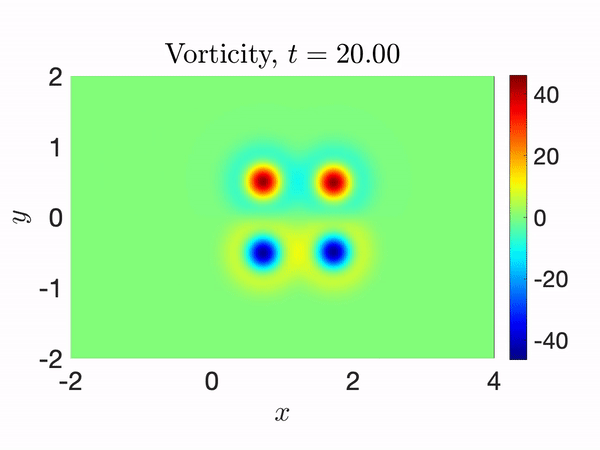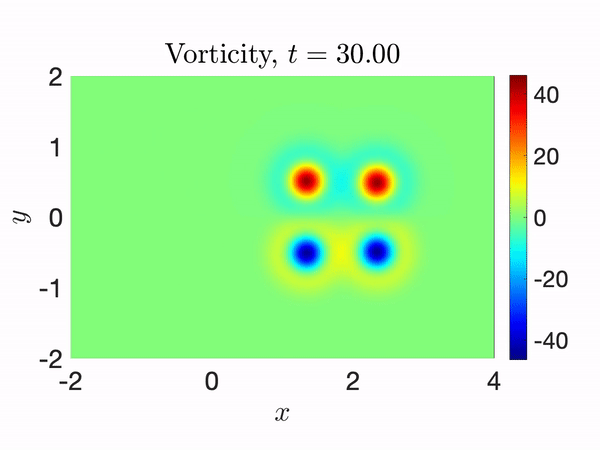
Leapfrogging vortices captured with RONS
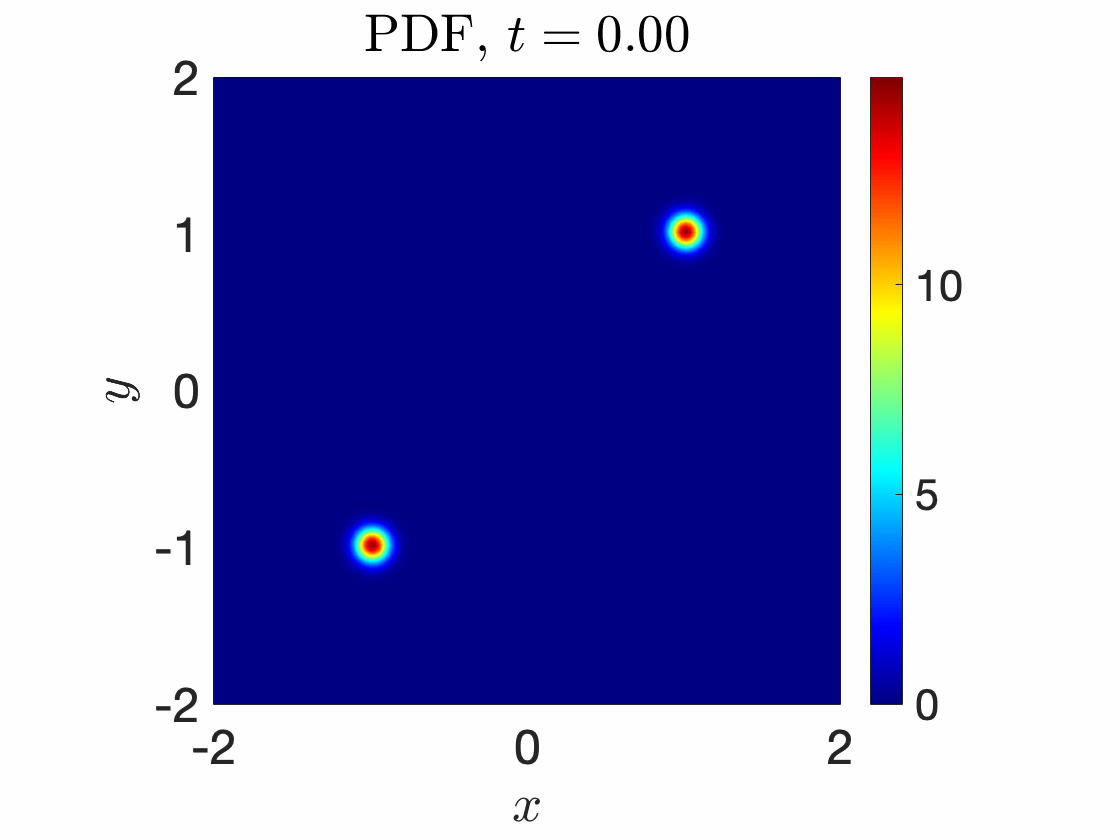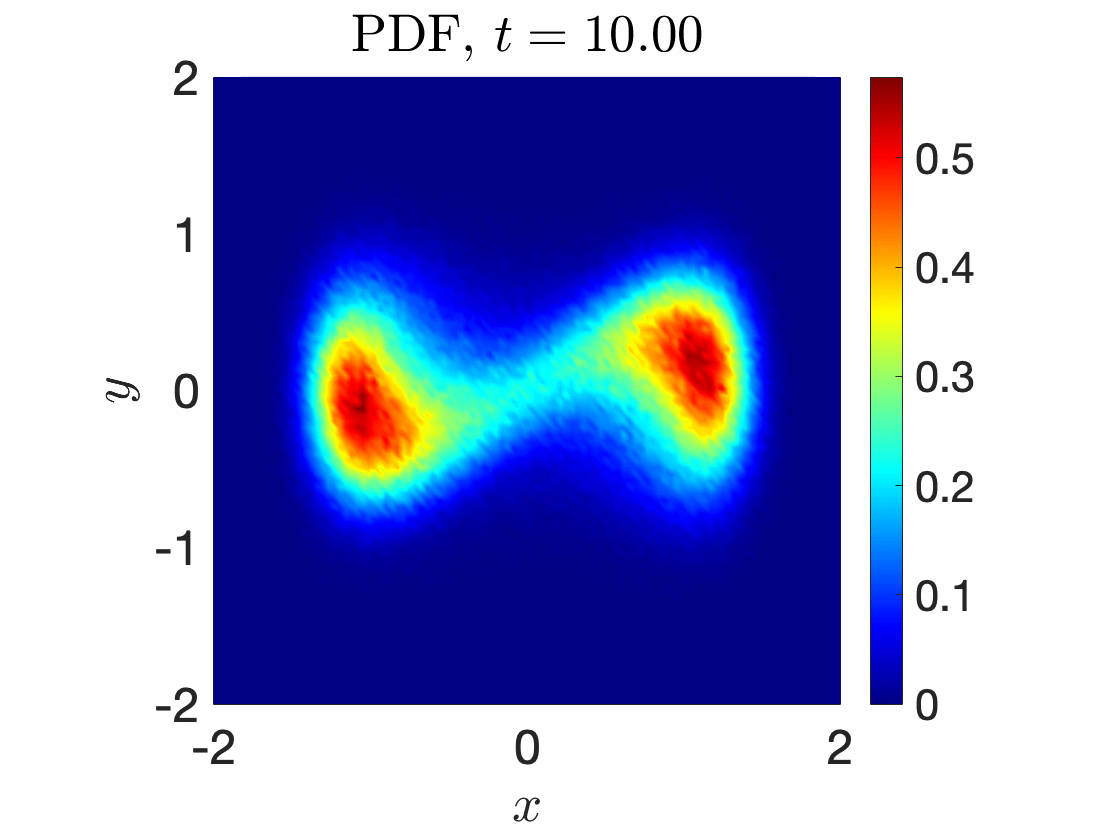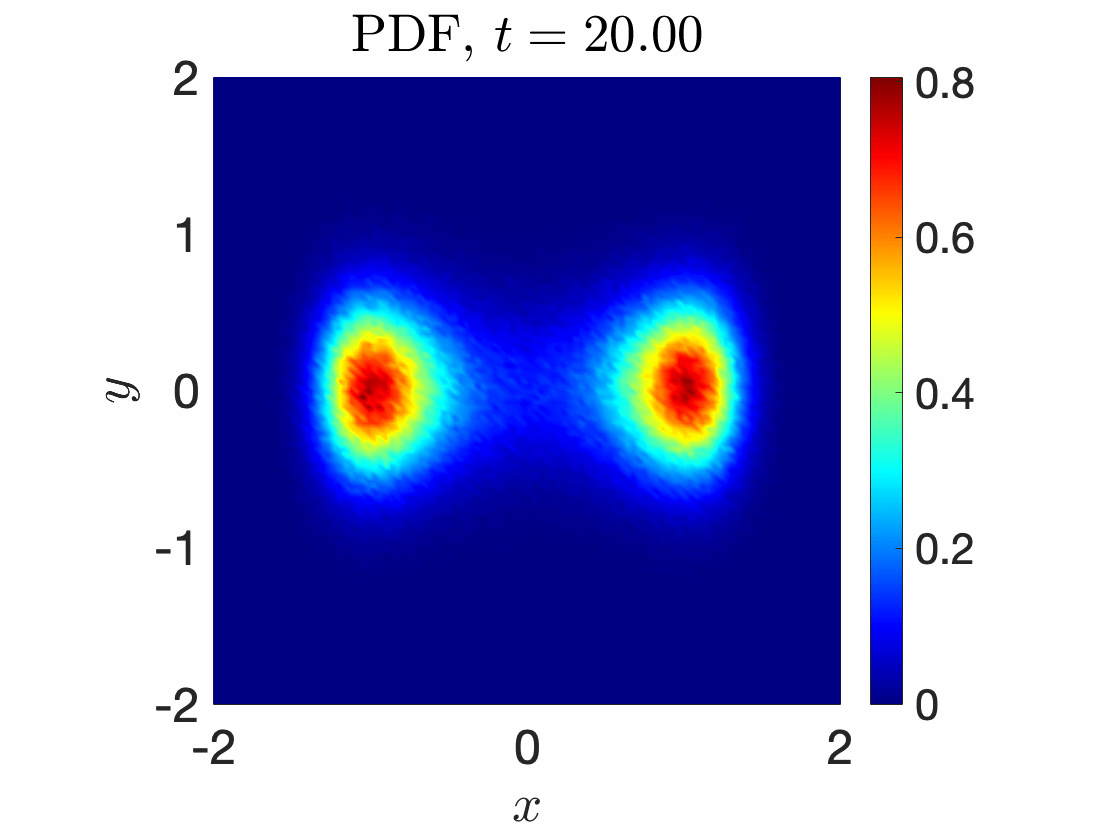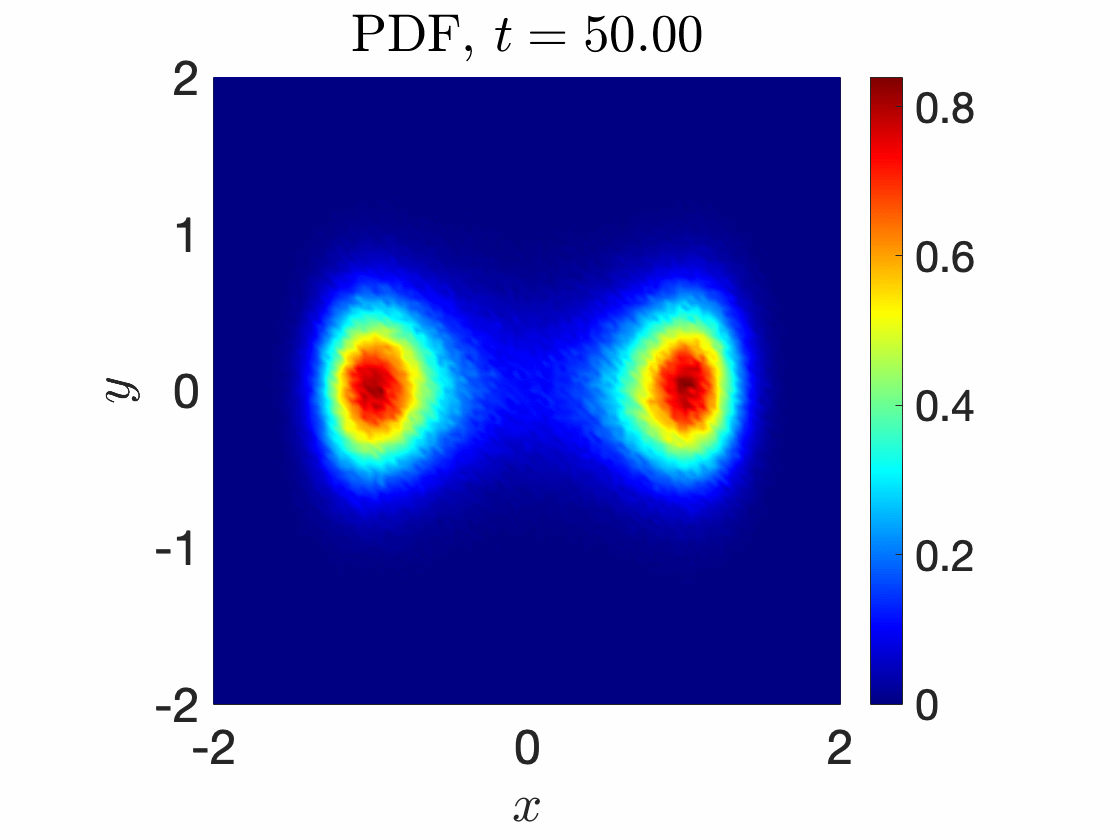 |  |
Stochastic Duffing oscillator with (left) Monte Carlo simulations (right) RONS
Publications:
W. Anderson, M. Farazmand. \Fisher information and shape-morphing modes for solving the Fokker-Planck equation in higher dimensions.Submitted. [https://arxiv.org/abs/2306.03749]
W. Anderson, M. Farazmand. Fast and scalable computation of reduced-order nonlinear solutions with application to evolutional neural networks. Submitted. [https://arxiv.org/abs/2207.13828]
W. Anderson, M. Farazmand. Shape-morphing reduced-order models for nonlinear Schrödinger equations. Nonlinear Dynamics, vol. 108, pp. 2889–2902, 2022 [https://arxiv.org/abs/2201.07953]
W. Anderson, M. Farazmand. Evolution of nonlinear reduced-order solutions for PDEs with conserved quantities. SIAM J. on Scientific Computing, vol. 44, pp. A176-A197, 2022 [https://arxiv.org/abs/2104.13515]
A geomorphic enthalpy method (undergraduate)
We extended an enthalpy method from heat transfer in order to model the behavior of fluvial river deltas. The problem is analogous to a Stefan problem, but with a latent heat that varies in space and time.
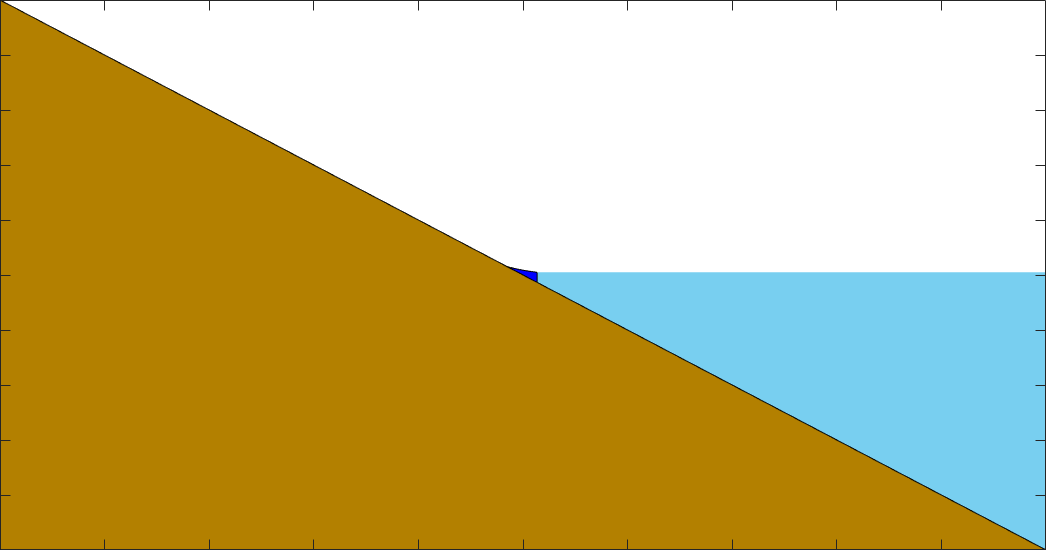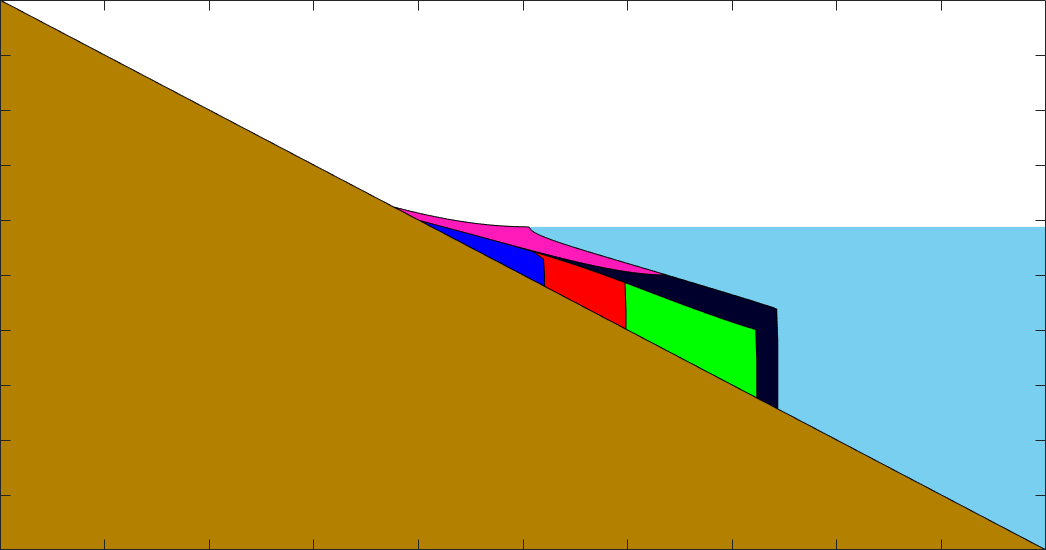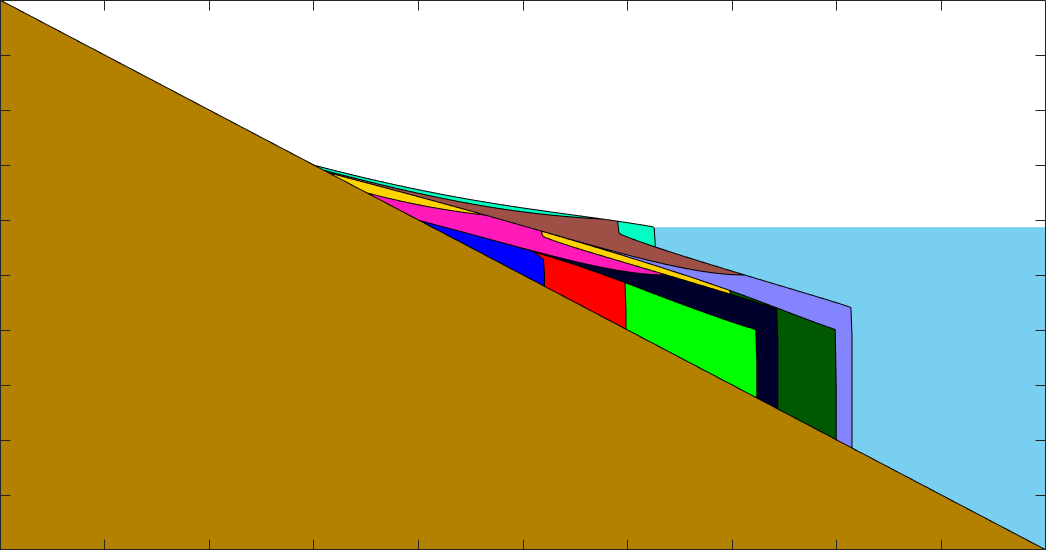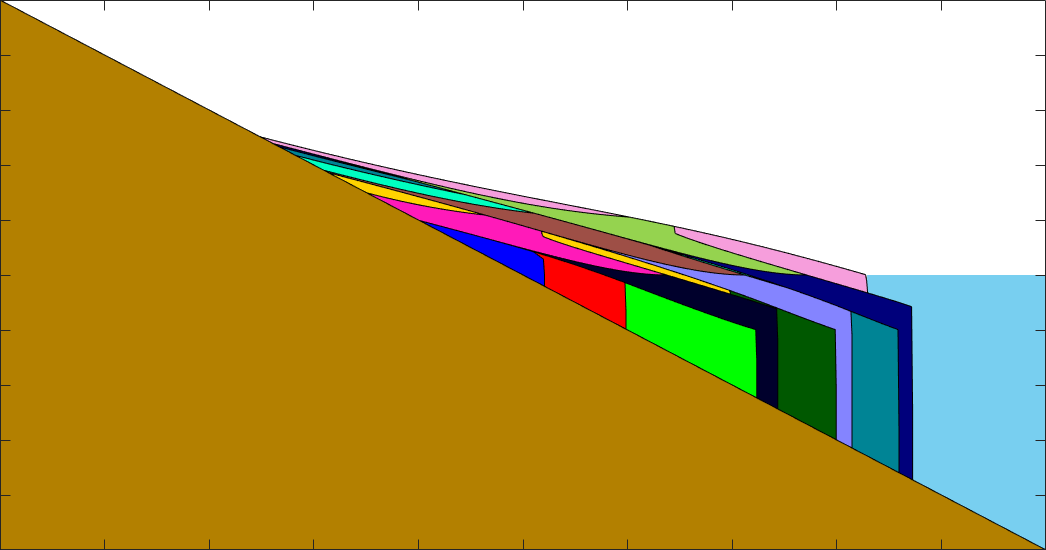

Publications:
W. Anderson, J. Lorenzo-Trueba, V.R. Voller. A geomorphic enthalpy method: Description and application to the evolution of fluvial-deltas under sea-level cycles. Computers & Geosciences, vol. 130, pp. 1-10, 2019
